Numerisches Lösen der Geodätengleichung mittels eines C/C++ Programmes
In Vorlesung 3 hatten wir die Geodätengleichung (bzw. das im unteren Bild dargestellte System von gekoppelten Differentialgleichungen zweiter Ordnung) mittels eines Python Jupyter Notebooks hergeleitet und danach unter Zuhilfenahme der im Python Modul 'scipy' definierten Funktion "odeint(DGLsys, initialval, tauval)" numerisch gelöst. In diesem neuen Unterpunkt werden wir die Geodätengleichung mittels eines C/C++ Programmes lösen (die Vorgehensweise dabei basiert auf dem in der Vorlesungsreihe Einführung in die Programmierung für Studierende der Physik (SS 2022) vorgestellten C++-Programm DGL_2.cpp. Das numerische Lösen von Differentialgleichungen ist ein mathematisch anspruchsvolles Thema und kann in dieser Vorlesung nicht im Detail erläutert werden. Bitte sehen Sie sich, bevor Sie weiterlesen, die folgende Seite an: Systeme von gekoppelten Differentialgleichungen und Differentialgleichungen zweiter Ordnung (SS 2022)
Die Geodätengleichung ist ein System von vier gekoppelten Differentialgleichungen zweiter Ordnung, welches man in ein System von acht gekoppelten Differentialgleichungen erster Ordnung umschreiben und dann numerisch lösen kann. In diesem Unterpunkt beschränken wir uns auf eine Schwarzschild-Raumzeit (nicht-rotierendes, nicht-geladenes Schwarzes Loch). Aufgrund der sphärischen Symmetrie der Schwarzschild-Raumzeit kann man sich bei der Beschreibung auf ebene, äquatoriale Bewegungen beschränken ($\theta=\frac{\pi}{2}, {\rm cos}(\theta)=0, {\rm sin}(\theta)=1, \frac{d \theta}{d\tau}=0, \frac{d^2 \theta}{d\tau^2}=0$). Dies hat zur Folge, dass eine der vier Differentialgleichungen trivial ist und man somit effektiv 'nur' sechs gekoppelte Differentialgleichungen erster Ordnung zu lösen hat. Im dem folgenden Unterpunkt leiten wir zunächst das Differentialgleichung-System der Geodätengleichung mittels eines Python Jupyter ab und exportieren es dann in ein C++ Programm. Das C++ Programm, wird dann im darauf folgenden Unterpunkt erläutert. Abschließend werden die Ergebnisse vorgestellt und diskutiert.
Analytische Herleitung des DGL Systems mittels Python Jupyter
Zunächst müssen wir das Differentialgleichung-System der Geodätengleichung in eine für das C++-Programm verständliche Form bringen. Wir benutzen dazu das Jupyter Notebook: GeodSchwarzschildII.ipynb und exportieren dann die Gleichungen des gekoppelten Differentialgleichung-Systems in C-Ausdrücke. Wie schon erwähnt betrachten wir eine ebene Bewegung des Probekörpers um ein Schwarzes Loch, wobei nur drei der vier Geodätengleichungen relevant sind (siehe linkes unteres Bild):


Um dieses System von drei gekoppelten Differentialgleichungen zweiter Ordnung mit Python nummerisch lösen zu können, müssen wir es zunächst in ein System von sechs Differentialgleichungen erster Ordnung umschreiben. Wir definieren dazu formal $$ t(\tau) = y_1(\tau) \, , \quad r(\tau) = y_2(\tau), \quad \phi(\tau) = y_3(\tau) \, , \quad \frac{d t(\tau)}{d\tau} = y_4(\tau) \, , \quad \frac{d r(\tau)}{d\tau} = y_5(\tau), \quad \frac{d \phi(\tau)}{d\tau} = y_6 $$ und schreiben unser DGL-System um (siehe rechtes oberes Bild).
Die oben ausgegebenen Ausdrücke werden nun in das C++-Programm integriert.
Das C++ Programm zum Lösen der Geodätengleichung
Als Vorlage verwenden wir das C++-Programm DGL_2.cpp und implementieren zunächst die ausgegebenen Ausdrücke in sechs DGL-bestimmenden C++-Funktionen

In der main()-Funktion des Programmes werden am Anfang die nötigen Variablen definiert, die man für die Euler bzw. Runge-Kutta Ordnung vier Methode benötigt. Die nötigen sechs Anfangswerte $\alpha_i(\tau = 0) \, , \, i=1,2,..6$ werden dem Beispiel des Jupyter Notebooks GeodSchwarzschildII.ipynb entnommen. Die Simulation der Bewegung des Probekörpers erfolgt in einem Eigenzeit-Intervall $[a,b]=[0,800]$, wobei wir $N=10000$ Gitterpunkte verwenden.

Die Beschreibung der während der Simulation im Terminal ausgegebenen Größen wird au-erhalb der Berechnung-Schleife (for-Schleife) gemacht. Die for-Schleife verläuft über die einzelnen $\tau$-Gitterpunkte und verwendet die Euler bzw. Runge-Kutta Ordnung vier Methode zum Lösen des DGL-Systems.


An jedem Eigenzeit-Gitterpunkt werden die berechneten Größen im Terminal ausgegeben. Nach Kompilierung des Programms (siehe links nebenstehende Abbildung) erhält man die folgende Terminal-Ausgabe (siehe unteres Bild).


Mittels des oberen Terminal-Befehls leiten wir die Ausgabe in die Datei 'DGL_2_VARTC.dat' um.
Das gesamte C++ Programm können Sie sich unter folgendem Link herunterladen:
DGL_2_VARTC.cpp
Resultate der Simulation
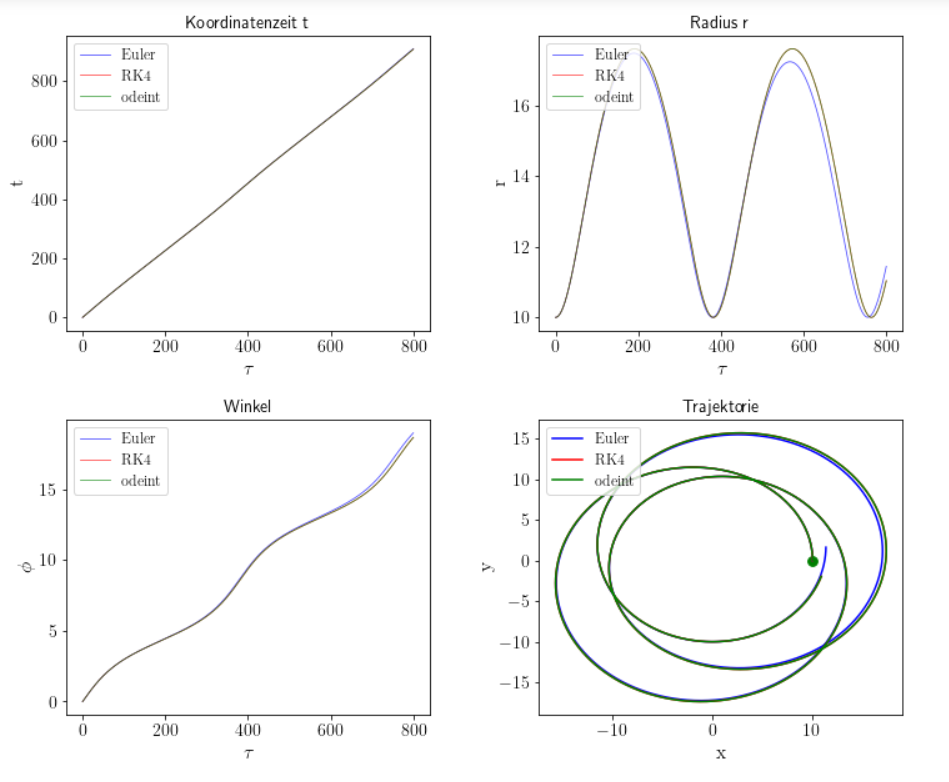
Beim Klicken auf das nebenstehende rechte Bild gelangen Sie zu dem Jupyter Notebook GeodSchwarzschildII.ipynb, in dem eine Visualisierung der Ergebnisse des oberen C++ Programms programmiert ist. Das Bild zeigt die Visualisierung der Daten von 'DGL_2_VARTC.dat' und vergleicht das Euler Verfahren mit der Runge-Kutta Ordnung vier Methode. Zusätzlich wird in der Abbildung auch die numerische Lösung, die in Python direkt generiert wurde (Methode "integrate.odeint()" im Python-Modul "scipy") mit den simulierten Daten der unterschiedlichen Verfahren verglichen.