3.6.1 Das freie mathematische Pendel

Zunächst werden wir uns einen Überblick darüber verschaffen, wie gut man die nichtlineare Rückstellkraft in einer Potenzreihe entwickeln kann. Man erhält bis zur 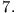Ordnung die Taylorreihe für

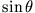Die Taylorreihe enthält nur ungerade Potenzen, da 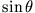ungerade bezüglich Spiegelung an der Ordinate ist. Wir sehen, dass eine lineare Näherung der Rückstellkraft erstaunlich gut gerechtfertigt ist für Winkel .

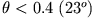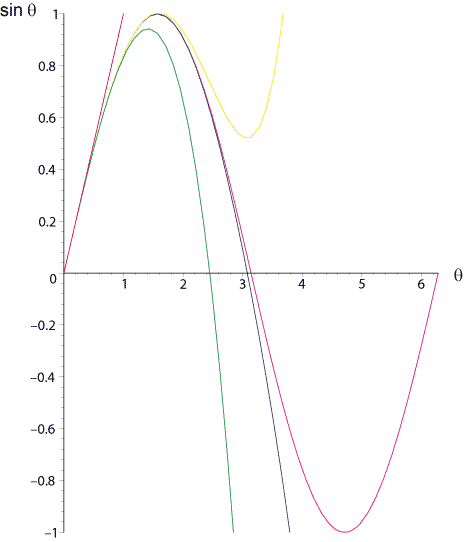
Abbildung 3.17: Taylorreihe von 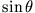. 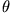(rot), 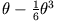(grün), 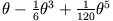(gelb), 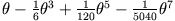(blau), exakt (magenta)

Mit wachsender Auslenkung sollte sich das mathematische Pendel von einem harmonischen Oszillator unterscheiden. Diesen Unterschied sieht man z.B. für die Anfangsbedingung 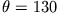in der folgenden Gegenüberstellung.

Abbildung 3.18: Mathematisches Pendel (grün) im Vergleich mit seiner linearen Näherung (blau).

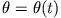
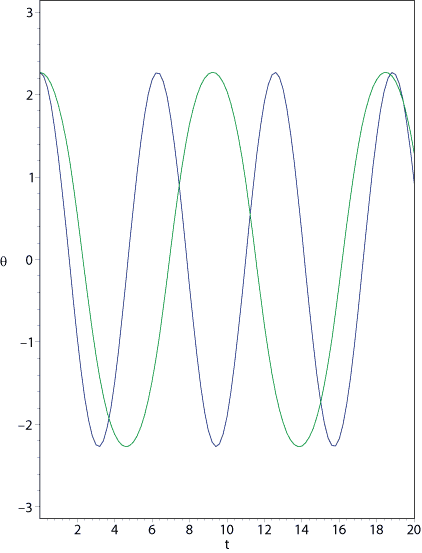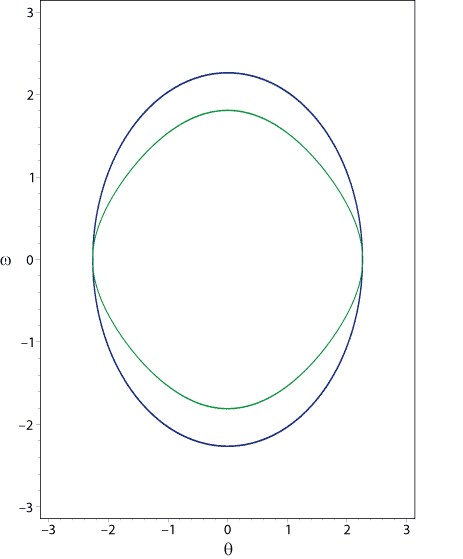
Abbildung 3.19: Phasenraumdiagramm des mathematischen Pendels (grün) und seiner linearen Näherung (blau).

Während das linearisierte Pendel (blau) durch eine trigonometrische Funktion beschrieben wird, erhält man für die nichtlineare Rückstellkraft (grün) eine elliptische Funktion als Lösung (siehe spezielle Funktionen der Theoretischen Physik). Die Frequenz des nichtlinearen Pendels ist abhängig von der Amplitude: mit wachsender Amplitude wird die Frequenz kleiner. Das Pendel hält sich viel länger in seinen Umkehrpunkten auf als der harmonische Oszillator.

Das mathematische Pendel ist ein konservatives System, d.h. seine mechanische Gesamtenergie

ist eine Erhaltungsgröße.

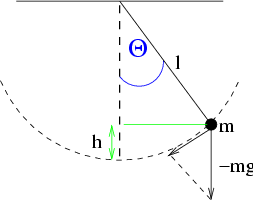
Abbildung 3.20: Potentielle Energie im Pendel

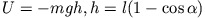
Wir wollen nun die Frage stellen, welche Bewegungsformen für das Pendel bei gegebener Gesamtenergie möglich sind. Dazu betrachten wir die Anfangsbedingung 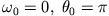, d.h. das Pendel befindet sich in dem labilen Gleichgewichtspunkt 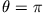. Die entsprechende Gesamtenergie ist in diesem Fall ()

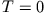Man sieht sofort, dass bei der geringsten zusätzlichen kinetischen Energie 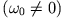, also für 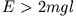, das System in einen Rotationszustand versetzt wird. Ist andererseits die potentielle Energie etwas geringer 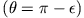, also 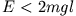, führt das System die gewohnte Pendelbewegung aus. 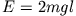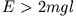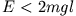Die Phasenraumtrajektorie für separiert offenbar den Phasenraum in zwei Teilräume: den Teilraum mit , in dem alle Anfangsbedingungen zu Rotatorlösungen führen und den Teilraum mit , in dem alle Anfangsbedingungen liegen, die eine Pendellösung initiieren. Dies führt uns zum Phasenraum Portrait des mathematischen Pendels. Befindet man sich mit der vorgegebenen Gesamtenergie in der Nähe der Separatrixlösung 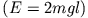, so kann eine kleine Änderung der Energie durch einen äußeren Antrieb spontan die Bewegungsform verändern und so zu einer komplizierten Phasenraumtrajektorie führen.

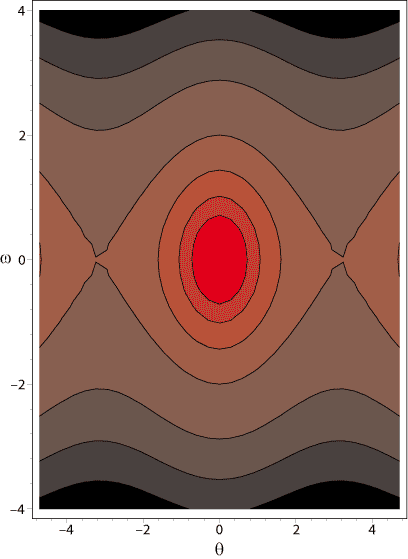
Abbildung 3.21: Phasenraum Portrait des mathematisches Pendels